Floats
Recall that a float, short for floating point number, is a real number with decimal precision. Use a float when you need an exact result that is not rounded down to the nearest integer.
Including the decimal . tells Python that a number is a float.

Approximations of π
Ancient mathematicians noticed that all circles had the same ratio between circumference and diameter, and it was only in the 18th century that this constant was commonly represented by the Greek letter π (pi).
One of the earliest approximations of π was as 22/7. Notice, combining a float with an integer produces a float.
Here are some other approximations of π over history.
25/8by the ancient Babylonians around the 18th century BC256/81by the ancient Egyptians around the 16th century BC339/108by Indian Vedic scholars around the 6th century BC377/120by Ptolemy, a Greco-Roman scholar, in the 2nd century BC3927/1250by Chinese mathematician Liu Hui in 263 AD62832/20000by Indian mathematician Aryabhata around 600 AD

Test It Out
Compare the accuracy of each of these approximations.

Temperature Conversions
Given a temperature C in degrees Celsius, print the temperature in degrees Fahrenheit as a float.
Note: The formula to convert celsius to fahrenheit is F = (9/5)C + 32.
Exponents
The exponent operator ** takes the number on the left side of the operator and raises it to the power of the number on the right side.

Finding e
The number e is a well-known constant that has many applications in mathematics. You can approximate the value of e by calculating (1 + (1/n))n for some large value of n.
Given a number n, print out an approximation of e by calculating the formula above.

Smallest Float
Every computer has a limit on how precise a floating point number can be.
If we divide by 10308 we get 10-308 which is a very small number, but it's still bigger than 0. If we divide by 10309 we just get 0 even though the correct answer would be 10-309.
Modulus
The modulus operator % returns the remainder after dividing the number on the left by the number on the right.
For example: 12 % 13 returns 12. This is because 12 / 13 is 0 with a remainder of 12.

Divisibility
A number a is evenly divisible by another number b if the result of a % b is 0.
If the remainder after dividing a by b is zero, then b is a factor of a, so a is divisible by b.

Divvying Up Candy
You have a certain amount of candy and a certain number of friends. After dividing the candy evenly amongst your friends (so each friend gets the same amount), print the amount of candy you have left for yourself. Your candy is the remainder after dividing candy by friends.

String Formatting
The modulus operator can also be used to insert values into a string.
The value 14 on the right of the % replaces %d in the string.

Inserting Strings
A string can be inserted into another string with the modulus operator and the %s pattern.

Inserting Numbers
An integer can be inserted into a string with the modulus and the %d pattern.
You can format a number to be inserted into k characters with the pattern %kd, where k is an integer. This is useful for aligning numbers when printing output.

Inserting Floats
You can format a floating point number with the %f pattern.
You can format a floating point number to print k digits after the decimal place with the pattern %.kf, where k is an integer.

Test It Out
Given a floating point number n and integer d, print n with d digits after the decimal place.
Incrementing and Decrementing

Incrementing
A variable's value can be used in calculating its new value. When assigning a value to a variable with the += operator, Python takes the original value of x and adds the value from the right side of the operator, in this case 1.
In the example below, the value of x is replaced by the result of x + 1, a process called incrementing.

Decrementing
When a variable is replaced by a smaller value, the process is called decrementing.
Change over time
A programmer is 60 inches tall and grows 5 inches a year. Suppose we want to calculate their height after a certain number of years.
One way to solve this problem is to initialize a variable height to the initial height of 60 inches. For each year, we increment the programmer's height by 5 inches, and print it out.
Notice: You have to first initialize a variable before you can increment it.

New Heights
Suppose the programmer's height changes by 4 inches in the first year, 6 inches in the second, and 3 inches in the third year. What would the programmer's height be in each year?
More On Increment and Decrement
You can increment or decrement a variable with any other operator.

Bacteria Population
The population of bacteria in a petri dish doubles every hour. Given the initial number of bacteria in the petri dish, print how many there will be after 1 hour, 2 hours, and 5 hours.

Sea Levels
Sea levels are rising because of the addition of water from melting glaciers and the expansion of sea water as it warms.
- Between 1995 and 2000, sea levels rose 9.83 mm.
- Between 2000 and 2005, sea levels rose 28.62 mm.
- Between 2005 and 2010, sea levels rose 45.58 mm.
- Between 2010 and 2015, sea levels rose 63.09 mm.
For the year 2000, 2005, 2010, and 2015, print out the total sea level rise from the 1995 sea level. Print each line in the format "Between 1995 and year, sea levels rose by amount mm."
Remember: Format your result with spaces and a period at the end of each sentence.
Mathematical Patterns

Fibonacci Sequence
Leonardo Bonnaci, also known as Fibonacci, came upon a sequence of numbers with remarkable properties when observing the growth of rabbit populations. The first two numbers of the sequence are 1, and each subsequent number is the sum of the two previous numbers.
1 1 2 3 5 8 13 21 34 55 ... n
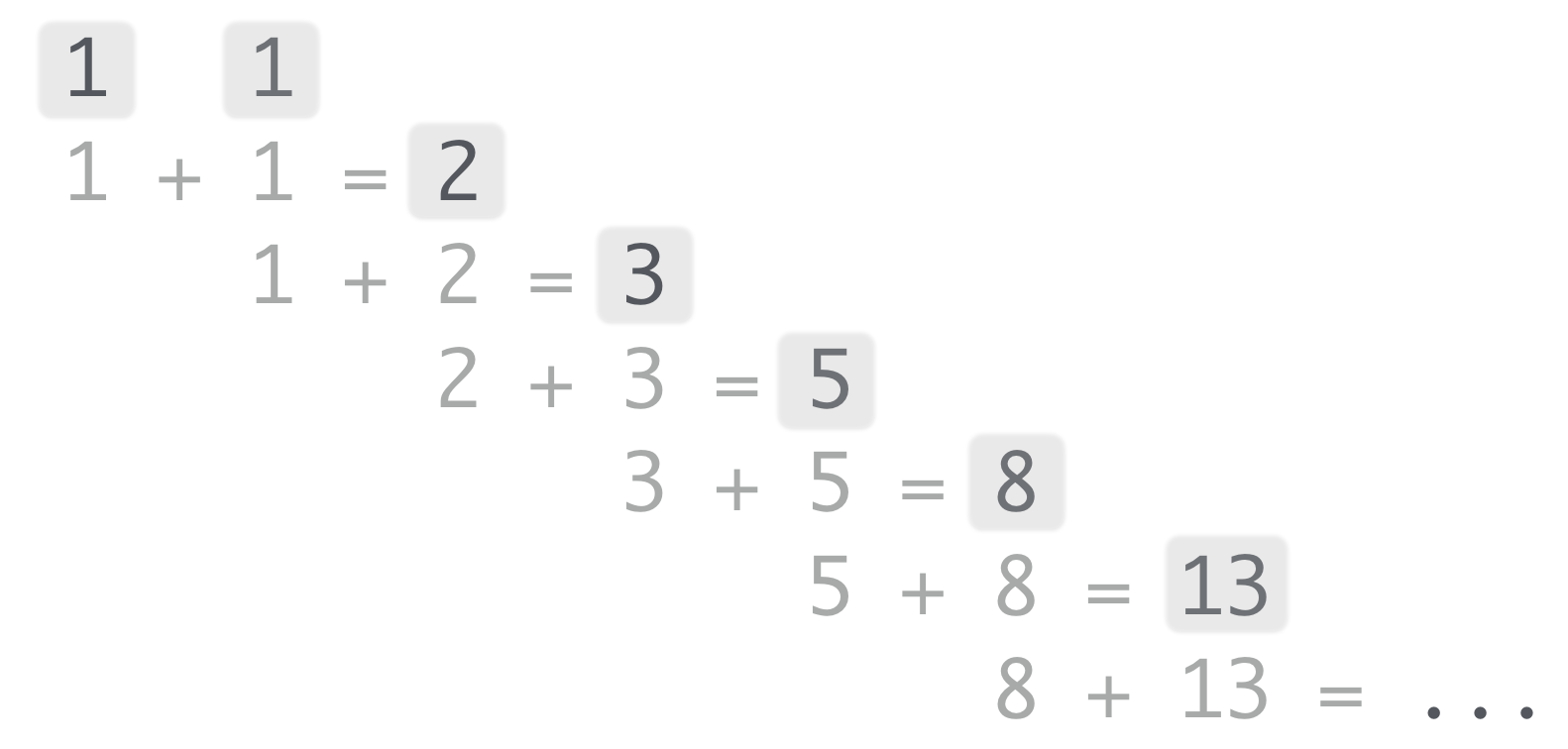
Use a loop and incrementing operators to print the nth number of the fibonacci sequence.

Golden ratio
Fibonacci noticed that the ratio between successive terms of the sequence came closer and closer to a special number in mathematics called the golden ratio, which is approximately 1.618033.
How accurately can you approximate the golden ratio with Fibonacci numbers?